Table of Contents
Bayesian Aggregation
Yang, Y., & Dunson, D. B., Minimax Optimal Bayesian Aggregation 2014 (arXiv)
Say we have a number of estimators \(\hat f_1, \ldots, \hat f_K\) derived from a number of models \(M_1, \ldots, M_K\) for some regression problem \(Y = f(X) + \epsilon\), but, as is the nature of things when estimating with limited data, we don’t know which estimator represents the true model (assuming the true model is in our list). The Bayesian habit is to stick a prior on the uncertainty, compute posteriors probabilities, and then average across the unknown parameter using the posterior probabilities as weights. Since the posterior probabilities (call them \(\lambda_1, \ldots, \lambda_K\)) have to sum to 1, we obtain a convex combination of our estimators \[ \hat f = \sum_{1\leq i \leq K} \lambda_i \hat f_i \] This is the approach of Bayesian Model Averaging (BMA). Yang et al. propose to find such combinations using a Dirichlet prior on the weights \(\lambda_i\). If we remove the restriction that the weights sum to 1 and instead only ask that they have finite sum in absolute value, then we obtain \(\hat f\) as a linear combination of \(\hat f_i\). The authors then place a Gamma prior on \(A = \sum_i |\lambda_i|\) and a Dirichlet prior on \(\mu_i = \frac{|\lambda_i|}{A}\). In both the linear and the convex cases they show that the resulting estimator is minimax optimal in the sense that it will give the best worst-case predictions for a given number of observations, including the case where a sparsity restriction is placed on the number of estimators \(\hat f_i\); in other words, \(\hat f\) converges to the true estimator as the number of observations increases with minimax optimal risk. The advantage to previous non-bayesian methods of linear or convex aggregation is that the sparsity parameter can be learned from the data. The Dirichlet convex combination gives good performance against Best Model selection, Majority Voting, and SuperLearner, especially when there are both a large number of observations and a large number of estimators.
I implemented the convex case in R for use with brms. The Dirichlet distribution has been reparameterized as a sum of Gamma RVs to aid in sampling. The Dirichlet concentration parameter is \(\frac{\alpha}{K^\gamma}\); the authors recommend choosing \(\alpha = 1\) and \(\gamma = 2\).
convex_regression <- function(formula, data,
family = "gaussian",
## Yang (2014) recommends alpha = 1, gamma = 2
alpha = 1, gamma = 2,
verbose = 0,
...) {
if (gamma <= 1) {
warning(paste("Parameter gamma should be greater than 1. Given:", gamma))
}
if (alpha <= 0) {
warning(paste("Parameter alpha should be greater than 0. Given:", alpha))
}
## Set up priors.
K <- length(terms(formula))
alpha_K <- alpha / (K^gamma)
stanvars <-
stanvar(alpha_K,
"alpha_K",
block = "data",
scode = " real<lower = 0> alpha_K; // dirichlet parameter"
) +
stanvar(
name = "b_raw",
block = "parameters",
scode = " vector<lower = 0>[K] b_raw; "
) +
stanvar(
name = "b",
block = "tparameters",
scode = " vector[K] b = b_raw / sum(b_raw);"
)
prior <- prior("target += gamma_lpdf(b_raw | alpha_K, 1)",
class = "b_raw", check = FALSE
)
f <- update.formula(formula, . ~ . - 1)
if (verbose > 0) {
make_stancode(f,
prior = prior,
data = data,
stanvars = stanvars
) %>% message()
}
fit_dir <- brm(f,
prior = prior,
family = family,
data = data,
stanvars = stanvars,
...
)
fit_dir
}
Here is a gist that includes an interface to parsnip.
In my own experiments, I found the performance of the convex aggregator to be comparable to a LASSO SuperLearner at the cost of the lengthier training that goes with MCMC methods and the finicky convergence of sparse priors. So I would likely reserve this for when I had lots of features and lots of estimators to work through, where I presume it would show an advantage. But in that case it would definitely be on my list of things to try.
Bayesian Stacking
Yao, Y., Vehtari, A., Simpson, D., & Gelman, A., Using Stacking to Average Bayesian Predictive Distributions (pdf)
Another approach to model combination is stacking. With stacking, model weights are chosen by cross-validation to minimize RMSE predictive error. Now, BMA finds the aggregated model that best fits the data, while stacking finds the aggregated model that gives the best predictions. Stacking therefore is usually better when predictions are what you want. A drawback is that stacking produces models through point estimates. So, they don’t give you all the information of a full distribution like BMA would. Yao et al. propose a method of stacking that instead finds the optimal predictive distribution by convex combinations of distributions with weights chosen by some scoring rule: the authors use the minimization of KL-divergence. Hence, they choose weights \(w\) empirically through LOO by \[ \max_w \frac{1}{n} \sum_{1\leq i \leq n} \log \sum_{1\leq k \leq K} w_k p(y_i | y_{-i}, M_k) \] where \(y_1, \ldots, y_n\) are the observed data and \(y_{-i}\) is the data with \(y_i\) left out. The following figure shows how stacking of predictive distributions gives the “best of both worlds” for BMA and point prediction stacking.
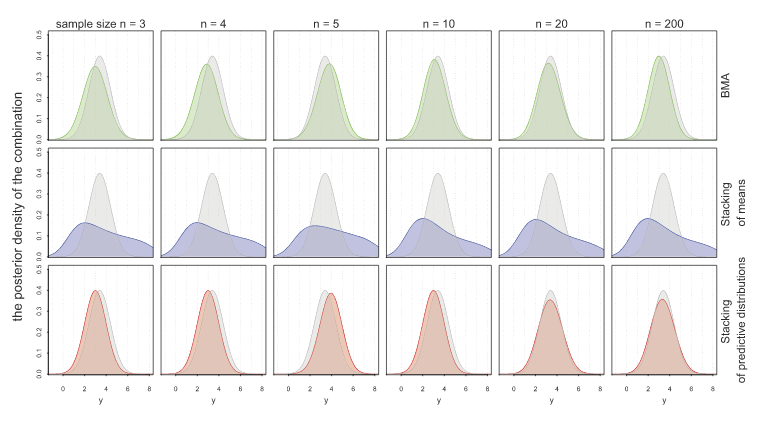
They have implemented stacking for Stan models in the R package loo.