We share a philosophy about linear algebra: we think basis-free, we write basis-free, but when the chips are down we close the office door and compute with matrices like fury.

Irving Kaplansky

Often, the first step in analyzing a problem is to transform it into something more amenable to our analysis. We would like the representation of our problem to reflect as naturally as possible whatever features of it we are most interested in. We might normalize data through a scaling transform, for instance, to eliminate spurious differences among like quantities. Or we might rotate data to align some of its salient dimensions with the coordinate axes, simplifying computations. Many matrix decompositions take the form \(M = BNA\). When \(B\) and \(A\) are non-singular, we can think of \(N\) as being a simpler representation of \(M\) under coordinate transforms \(B\) and \(A\). The spectral decomposition and the singular value decomposition are of this form.

All of these kinds of coordinate transformations are linear transformations. Linear coordinate transformations come about from operations on basis vectors that leave any vectors represented by them unchanged. They are, in other words, a change of basis.

This post came about from my frustration at not finding simple formulas for these transformations with simple explanations to go along with them. So here, I tried to give a simple exposition of coordinate transformations for vectors in vector spaces along with transformations of their cousins, the covectors in the dual space. I’ll get into matrices and some applications in a future post.

Vectors

Example - Part 1

Let’s go through an example to see how it works. (I’ll assume the field is \(\mathbb{R}\) throughout.)

Let \(e\) be the standard basis in \(\mathbb{R}^2\) and let \(e'\) be another basis where \[ \begin{array}{cc} e'_1 = \frac12 e_1, & e'_2 = -e_1 + 2 e_2 \end{array} \] So we have written the basis \(e'\) in terms of the standard basis \(e\). As vectors they look like this:

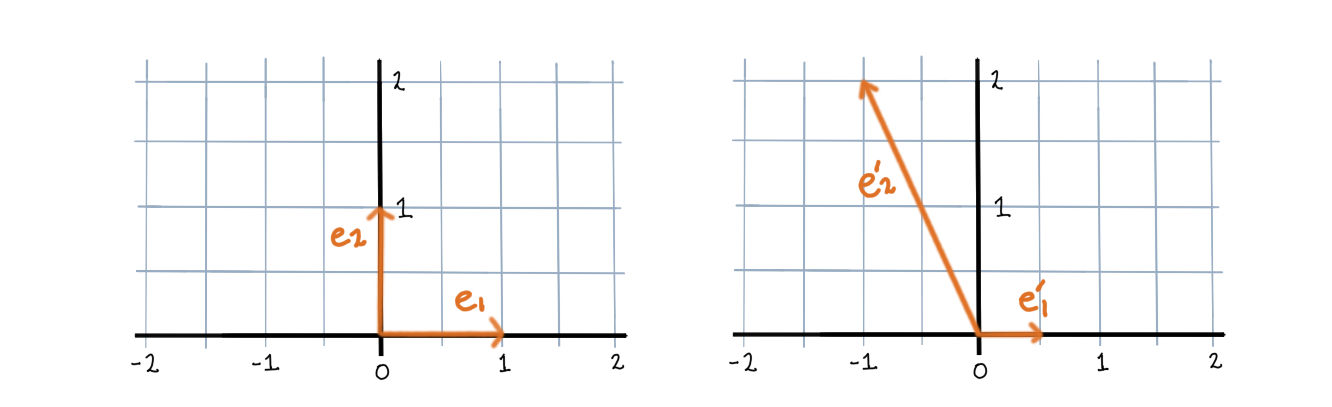
And each will induce its own coordinate system, indicating the angle and orientation of each axis, and each axis’ unit of measure.

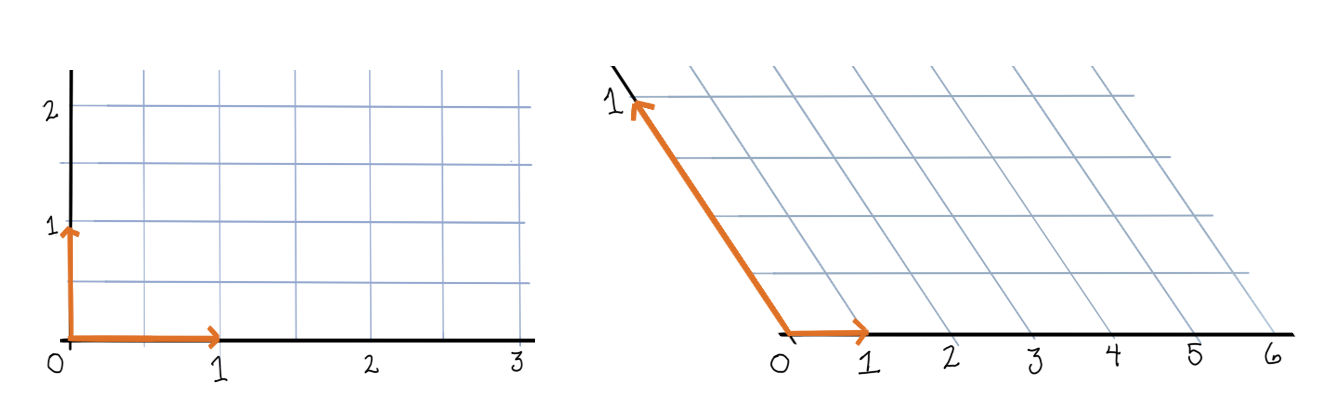
We can write any vector in \(\mathbb{R}^2\) as a linear combination of these basis elements.

\[\begin{array}{cc} v = e_1 + 2 e_2, & w' = 5 e'_1 + \frac12 e'_2 \end{array}\]

We call the coefficients on the basis elements the coordinates of the vector in that basis. So, in basis \(e\) the vector \(v\) has coordinates \((1, 2)\), and in basis \(e'\) the vector \(w'\) has coordinates \((5, \frac12)\).

Formulas

The choice of basis is just a choice of representation. The vector itself should stay the same. So the question is – how can we rewrite a vector in a different basis without changing the vector itself?

Let’s establish some notation. First, whenever we are talking about a vector in the abstract, let’s write \(\mathbf{v}\), and whenever we are talking about a vector represented in some basis let’s write \(v\). So the same vector \(\mathbf{v}\) might have two different basis representations \(v\) and \(v'\), which nevertheless all stand for the same vector: \(\mathbf{v} = v = v'\). However, when we write \(e\) for a basis, we mean a list of vectors \(e_i\) that form a basis in some vector space \(V\). So, \(v = v'\) always, but in general \(e \neq e'\).

Our basis elements let’s index with subscripts (like \(e_1\)), and coordinates let’s index with superscripts (like \(v^1\)). This will help us keep track of which one we’re working with. Also, let’s write basis elements as row vectors, and coordinates as column vectors. This way we can write a vector as a matrix product of the basis elements and the coordinates:

\[v = \begin{bmatrix} e_1 & e_2 \end{bmatrix}\begin{bmatrix}v^1 \\ v^2\end{bmatrix} = v^1 e_1 + v^2 e_2 \]

Now we can also write the transformation given above of \(e\) into \(e'\) using matrix multiplication:

\[e' = \begin{bmatrix}e'_1& e'_2\end{bmatrix} = \begin{bmatrix}e_1& e_2\end{bmatrix}\begin{bmatrix} \frac12 & -1 \\ 0 & 2 \end{bmatrix} = \begin{bmatrix}\frac12 e_1 & -e_1 + 2 e_2\end{bmatrix}\]

The \(2 \times 2\) matrix used in that transformation is called the transformation matrix from the basis \(e\) to the basis \(e'\).

The general formula is

\[\formbox{e' = e A}\]

where \(A\) is the transformation matrix. We can use this same matrix to transform coordinate vectors, but we shouldn’t necessarily expect that we can use the same formula. The bases and the coordinates are playing different roles here: the basis elements are vectors that describe the coordinate system, while the coordinates are scalars that describe a vector’s position in that system.

Let’s think about how this should work. Generally we write \(v = v^1 e_1 + v^2 e_2 \cdots + v^n e_n\). If we make some new basis \(e'\) by multiplying all the \(e_i\)’s by 2, say, and also multiplied all the \(v_j\)’s by 2, then we would end up with a vector four times the size of the original. Instead, we should have multiplied all the \(v_j\)’s by \(\frac12\), the inverse of 2, and then we would have \(v' = v\), as needed. The vector must be the same in either basis.

So, if we change the \(e\)’s by some factor then, the \(v\)’s need to change in the inverse manner to maintain equality. This suggests that to change \(v\) into a representation \(v'\) in basis \(e'\) we should use instead

\[\formbox{v' = A^{-1} v}\]

(We’ll prove it a little bit later.)

The fact that basis elements change in one way (\(e' = e A\)) while coordinates change in the inverse way (\(v' = A^{-1} v\)), is why we sometimes call the basis elements covariant and the vector coordinates contravariant, and distinguish them with the position of their indices.

Example - Part 2

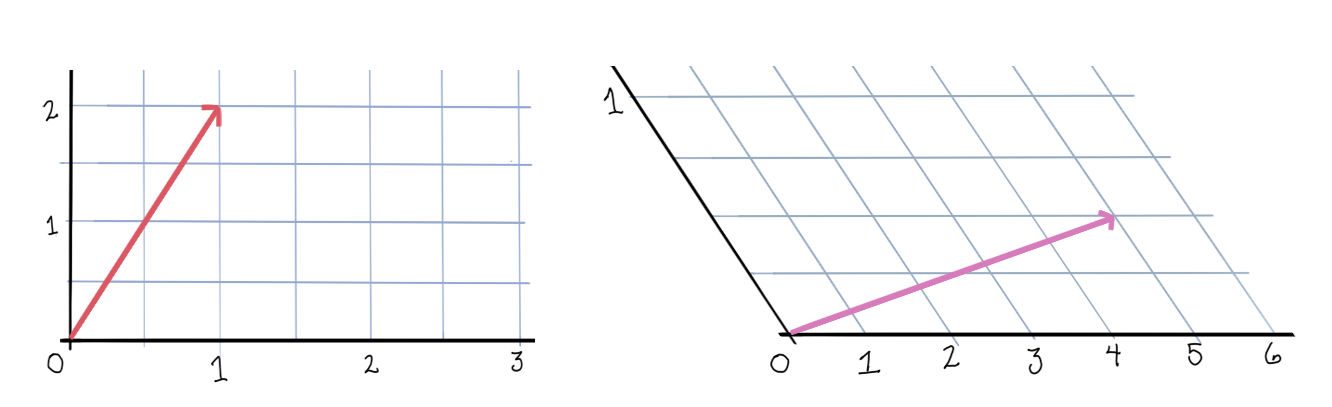
Let’s go back to our example. Using our formula, we get

\[ v' = \begin{bmatrix}2 & 1 \\ 0 & \frac12 \end{bmatrix} \begin{bmatrix}1 \\ 2\end{bmatrix} = \begin{bmatrix}4 \\ 1\end{bmatrix} \]

But what about \(w'\)? Well, since its representation is in \(e'\), to convert in the opposite direction, to \(e\), we need to use the transformation that’s the inverse of \(A^{-1}\), namely, \(A\).

\[ w = \begin{bmatrix}\frac12 & -1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix}5 \\ \frac12\end{bmatrix} = \begin{bmatrix}2 \\ 1\end{bmatrix} \]

And now we have:

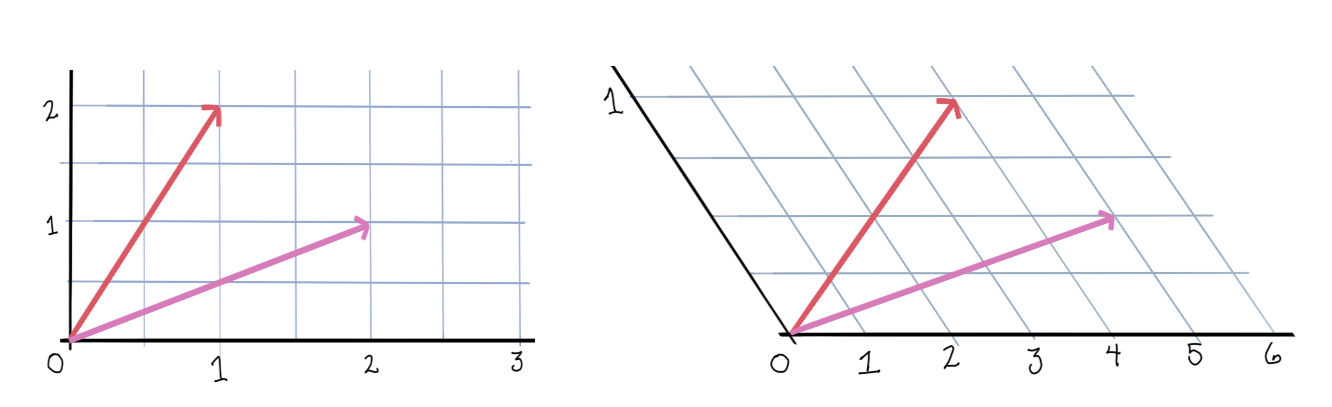
Each vector is unchanged after a change of basis.

Covectors

Recall the inner product on a vector space.

We might ask, given some vector \(v\) how does an inner product vary as we range over vectors \(w\)? In this case, we could think of \(\langle v, \cdot\rangle\) as a function of vectors in \(V\) whose outputs are scalars. In fact, these sorts of functions themselves form a vector space, called the dual space of \(V\), which we write \(V^*\). The members of \(V^*\) are called linear functionals or covectors. The covector given by \(\langle v, \cdot\rangle\) we denote \(v^*\).

We’ve been working with vectors in \(\mathbb{R}^n\), and in \(\mathbb{R}^n\) the (canonical) inner product is the dot product. This means that if we denote the covectors in \(V^*\) as rows and the vectors in \(V\) as columns (as usual), then we can write

\[ v^*(w) = \begin{bmatrix} v_1 & \cdots & v_n\end{bmatrix}\begin{bmatrix}w^1 \\ \vdots\\ w^n\end{bmatrix} = v_1 w^1 + \cdots + v_n w^n \]

So, the covectors are functions \(\mathbb{R}^n \to \mathbb{R}\), but we can do computations with them just like we do with vectors, using matrix multiplication. We still write the indices of the row vectors as subscripts and the indices of the column vectors as superscripts.

If we can think about vectors in \(\mathbb{R}^n\) as arrows, how should we think about covectors? To simplify things, let’s restrict our attention to the two-dimensional case. Now, consider the action of a covector \(v^*\) on some unknown vector \(w = \begin{bmatrix}x& y\end{bmatrix}^\top\) in \(\mathbb{R}^2\):

\[ v^*(w) = v_1 x + v_2 y \]

Now if we look at the level sets of this function, \(v_1 x + v_2 y = k\), it should start to look familiar…

It’s a family of lines!

And to find out the value of \(v^*(w)\) we just count how many lines of \(v^*\) the vector \(w\) passes through (including maybe “fractional” valued lines – \(k\) doesn’t have to just be an integer). More generally, the covectors of \(\mathbb{R}^n\) can be thought of as hyperplanes, and the value of \(v^*(w)\) can be determined by how many hyperplanes of \(v^*\) the vector \(w\) passes through. And furthermore, the vector \(v\) will be the normal vector to the hyperplanes given by \(v^*\), that is, they are perpendicular.

Example - Part 3

In the standard basis, let \(v^*\) be given by \(\begin{bmatrix}1 & 2\end{bmatrix}\). Its family of lines will then be \(x + 2 y = k\). Now let \(w\) be given by \(\begin{bmatrix}2 & 1\end{bmatrix}\), and count how many lines \(w\) crosses through:

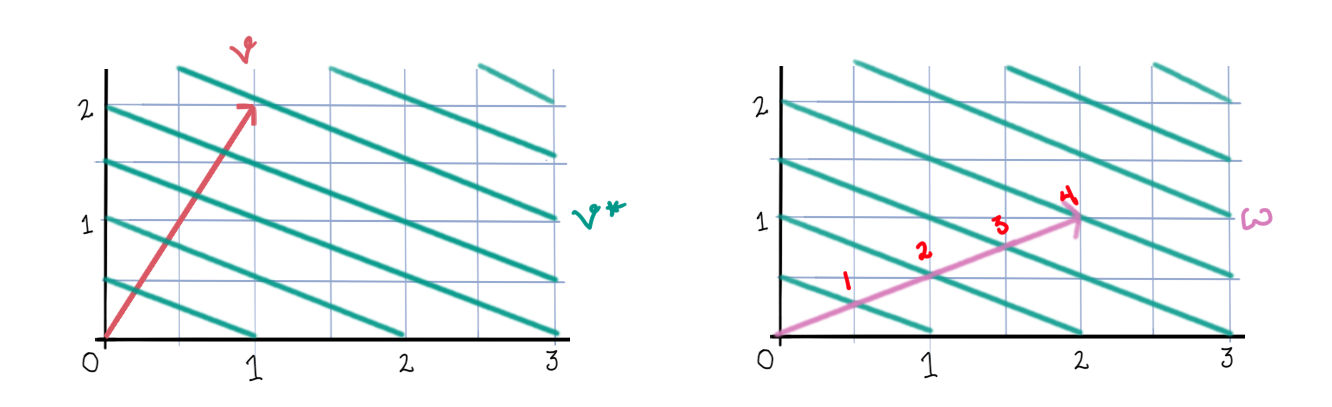
It’s exactly the same as \(v^*(w) = 2 + 2(1) = 4\)! I think that’s pretty cool.

The Dual Basis

Okay, so what about bases in \(V^*\)? We’d like to have a basis for \(V^*\) that is the “best fit” for whatever basis we have in \(V\). This turns out to be the basis given by: \[ e^i(e_j) = \begin{cases} 1 & \text{if } i = j\\ 0 & \text{if } i \ne j \end{cases}\]

where \((e_j)\) is a basis in \(V\). Or sometimes people write instead \(e^i(e_j) = \delta^i_j\), where \(\delta^i_j\) is the Kronecker delta. We call this basis \((e^i)\) the dual basis of \((e_j)\). You can see that a basis and its dual have a kind of “bi-orthogonality” property that turns out to be very convenient.

Let’s look at formulas for changing bases now. If we have a vector \(v\) in \(V\) written as a column, how can we find the corresponding vector \(v^*\) in \(V^*\)? The obvious thing to do would be to take the transposition of \(v\). This will not always work. Recall the definitions of \(v, v', w\) and \(w'\) from the first section, and consider:

\[v^\top v = \begin{bmatrix} 1 & 2\end{bmatrix}\begin{bmatrix}1 \\ 2\end{bmatrix} = 1 + 4 = 5\]

\[v'^\top v' = \begin{bmatrix} 4 & 1\end{bmatrix}\begin{bmatrix}4 \\ 1\end{bmatrix} = 16 + 1 = 17\]

This is no good. We get two different values for \(\bar v^*(\bar w)\) depending on which basis we use, but the values of a function on a vector space shouldn’t depend on the basis. The trouble is that the dual of \((e'_i)\) isn’t the transpose of those basis vectors (they don’t satisfy the bi-orthogonality property), so the duals of those vectors represented in it won’t be the transposes of those vectors either.

This will be true for orthonormal bases, however. The standard basis \((e_i)\) is orthonormal, and the duals of the vectors represented in it will in fact be those transposes.

\[ \formbox{v^* = v^\top \text{for any vector } v \text{ written in an orthonormal basis.}} \]

Formulas

The next question is, if we perform a change of basis in \(V\), what is the corresponding change in \(V^*\)? Let’s use the same reasoning that we did before. For a vector \(w\) in \(\mathbb{R}\) and a covector \(v^*\), we have

\[ v^*(w) = v_1 w^1 + \cdots + v_n w^n \]

And so, like before, if we change the values of the \(w_j\)’s, the values of the \(v^i\)’s should change in the inverse manner to preserve equality. But \(w\) changes as \(w' = A^{-1} w\), so \(v^*\) must change as \(v'^* = v^* A\). And its basis (the dual basis) must change as its inverse: \(e'^* = A^{-1} e^*\).

\[\formbox{\begin{align} e'^* &= A^{-1} e^*\\ v'^* &= v^* A \end{align}}\]

Notice that this time the basis vectors are playing the contravariant part, while the coordinates are playing the covariant part with respect to the original vector space.

Example - Part 4

Lets continue our example. Since \(e\) is the standard basis, it is orthonormal, and we can therefore find the duals of \(v\) and \(w\) by taking transposes. We can then apply our formula to find the duals of \(v'^*\) and \(w'^*\).

The duals too are unchanged after a change of basis.

Summary of Formulas

\[\formbox{\begin{array}{llr} e' &= e A & &(1)\\ v' &= A^{-1} v & &(2)\\ e'^* &= A^{-1} e^* & &(3)\\ v'^* &= v^* A & &(4) \end{array} }\]

Suppose \((1)\), that \(e' = e A\), where \(A\) is a non-singular matrix.

Proof of (2): We know \(e v = e' v'\). Now

\[ e' v' = e v = e A A^{-1} v = e' (A^{-1} v) \]

But then it must be that \(v' = A^{-1} v\) since basis representations are unique.

Proof of (4): We also know \(v'^* w' = v^* w\) for all vectors \(w\). But then

\[ v'^* w' = v^* w = v^* w = v^* A A^{-1} w = (v^* A) w' \]

for all \(w'\). So, \(v'^* = v^* A\).

Proof of (3): Lastly,

\[ v'^* e'^* = v^* e^* = v^* A A^{-1} e^* = v'^* A^{-1} e^* \]

for all \(w'\). So, \(e'^* = A^{-1}e^*\). QED